일반적으로 사람이 사용하는 10진수(Decimal)과 다르게 컴퓨터에서는 2진수(Binary)의 Number System을 사용하는 것은 문과도 아는 사실이다.
1. Number, 즉 숫자를 표기할 때에는 부호(sign)와 크기(magnitude) 둘 다 존재하여야 한다. 부호로는 +/-를 의미하며, 크기는 50,100... 등을 의미함.
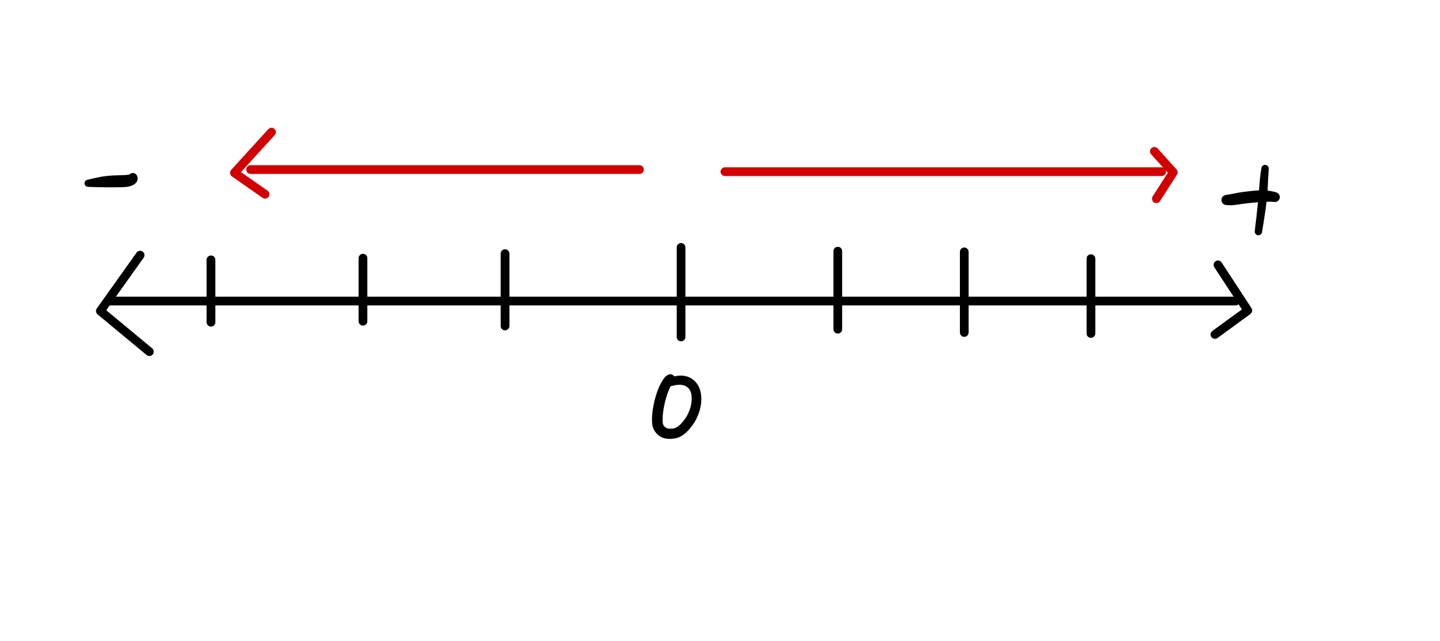
중학교 때부터 사용하는 수직선 표현이 위에 대한 설명의 형태이다.
2. 다음은 Character라는 것이 있는데 이는 symbol이다. 부호와 크기로 표현하는 것이 아닌 문자로 표현한다.
ex) ㄱ, ㄴ, A, B , ...
3-0
사람과 컴퓨터의 차이는 진수에서 발생하기도 하지만, 사람은 양수, 음수를 자유로이 표현하는 데에 반해, 컴퓨터는 부호가 아닌 오직 0과 1로만 판단을 한다.
따라서 컴퓨터가 부호를 판별할 때에도 0과 1로 구분을 짓는다. 0은 +를, 1은 -를 의미한다.
그리고 이 비트는 가장 중요한 비트라고 해서 MSB(=Most Significant Bit)라 말한다.
ex1) 010111는 MSB가 0이기 때문에 양수이다.
ex2) 111101은 MSB가 1이기 때문에 음수이다.
양수와 음수를 표현하는 방법
3-1 Signed Magnitude(SM)

위 표현은 3-0에서 기술했던 MSB로 표현한 수 표현이다. 빨간 줄은 부호(sign)을, 분홍 줄은 크기(magnitude)이다.
단순한 표현에서는 문제가 발생하지 않지만 아래 예시를 보면 적절한 방법이 아님을 알 수 있다.

<1> 은 양수끼리의 덧셈이다.
<2>은 음수와 양수의 덧셈인데 문제가 발생한다.
<3>은 음수끼리의 덧셈이며 마찬가지로 문제가 발생한다.(여기서 오버플로우는 생각하지 않습니다.)
※여기서 발생한 문제는 인간이 사용한 10진법과의 숫자가 일치하지 않음을 말한다.
따라서 위 방식으로는 산술에서 문제가 발생하기 때문에 적절하지 않은 표현이다.
3-2 1's complement (1의 보수)
우선 알아야 하는 용어가 보수인데, 주산을 배웠다면 알고 있을 용어이고, 안 배웠어도 어렵지 않은 개념이다.
보수란 말 그대로 보충하는 수를 말한다.
보수를 수학적으로 풀이하자면 각 진수를 만드는 수를 의미하며, 10진수는 각 수를 더해 10을 만들면 된다.
다음의 예시를 보자.
ex) 다음 수 4의 보수는 6이다.

1의 보수로 -9를 2진수로 표현했으며 MSB 표현 또한 충족한다.
주의할 점은 MSB가 1일 때에는 크기를 바로 알 수가 없다. 따라서 변환하는 과정이 필요한데, 1의 보수 표현을 되돌리기만 하면 된다.
Tip : 1의 보수 표현은 0을 1로, 1을 0으로 바꾸기만 하면 된다.
하지만, 위 방법에서도 문제가 발생하게 된다.
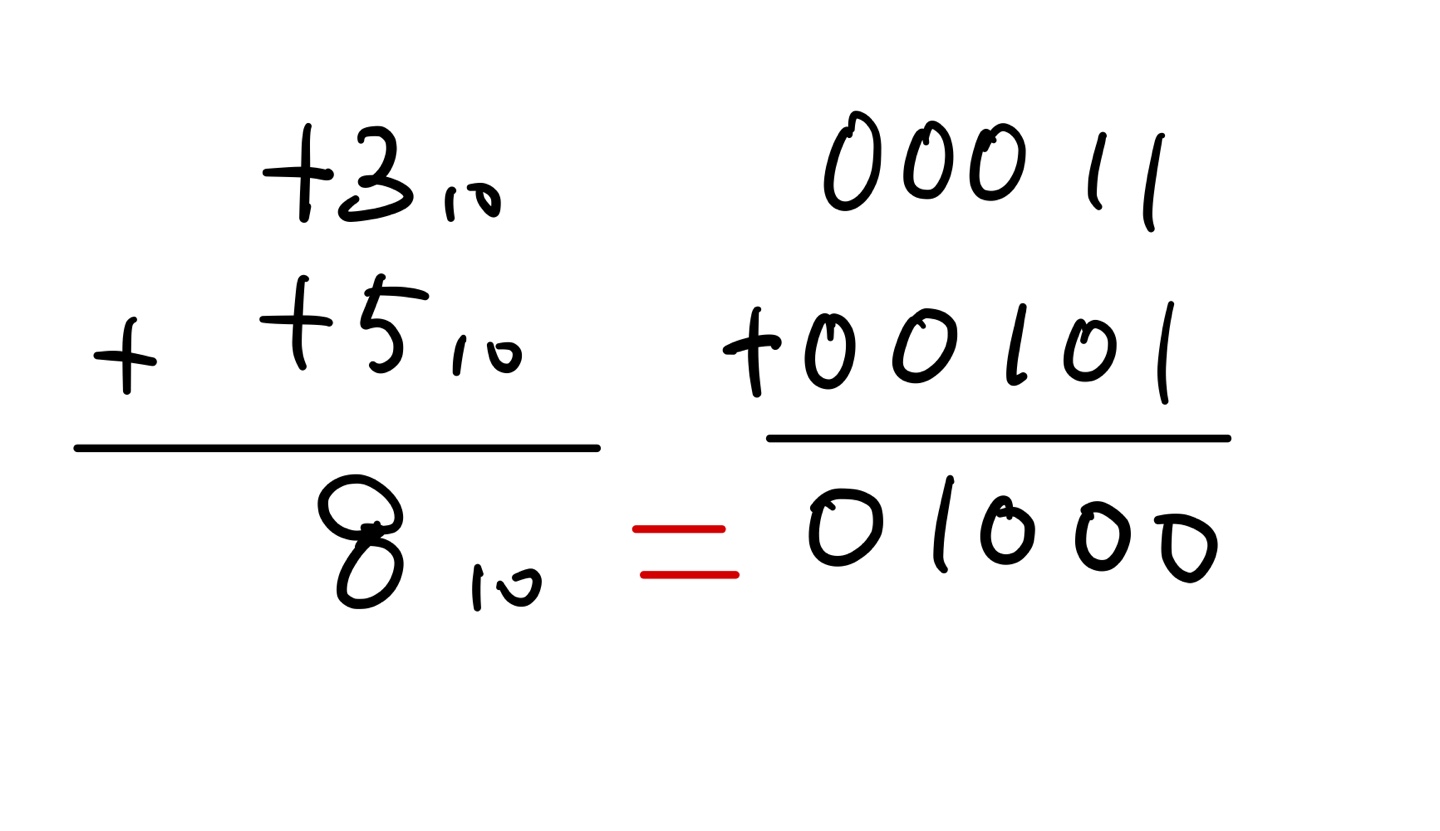

일반적인 산술에서 문제가 발생하지는 않지만, 산술의 결과가 0일 시에 문제가 발생하게 된다.
11111에서 MSB가 1이기 때문에 음수라는 것을 확인할 수 있는데 +0과 -0의 표현이 동일하지가 않다.
따라서 위 방법도 적절한 표현이 아니다.
3-3 2's complement (2의 보수)
이 방식을 표현하기 위하여 앞선 방법들을 소개한 것이며, 특히 1의 보수 개념을 알아야지만 사용할 수 있는 산술방법이다.
만드는 방식은 1의 보수를 취한 후에 1을 더해주기만 하면 된다.

-9를 만드는 방법이고
위에 기술하였듯이 주의할 점은 음수는 크기 파악을 바로 할 수 없다는 것이다.
음수라는 것이 파악됐으면 할 수 있는 것은 -를 달아주는 것 밖에 존재하지 않는다.
이후에 1's의 보수와 1을 더해야지만 비로소 크기를 알 수 있다.

위에서 -5를 2진수로 바로 적을 수 없기 때문에 반드시 +5에서 변환 과정을 가진다.
변환 후 산술을 하였을 때에, 11110의 수가 나오며 여기서는 -를 달아주는 것 밖에 할 수가 없다.
마찬가지로 변환과정으로 크기 2를 도출한 후에 -2라는 것이 파악 가능하다.

1의 보수와 다르게 +0과 -0에서 0000으로 표현이 동일하다.
따라서 어떠한 산술에서도 문제가 발생하지 않기 때문에, 2의 보수 방법을 사용하는 것이 옳다.
'대학과목 정리 > 디지털회로' 카테고리의 다른 글
| [Chapter 2 - 2] 부울 대수의 정리 (0) | 2021.08.02 |
|---|---|
| [Chapter 2-1] 부울 대수의 공리 [Boolean Algebra] (0) | 2021.07.01 |
| 디지털회로 (0) | 2021.06.29 |